Construcțiile auxiliare sunt folosite în geometrie pentru a oferi o nouă perspectivă asupra figurii.
Exemplu din viața reală: vrei să vorbești simultan cu mama și cu tata pe viu. Fiecare este într-o altă cameră. Cum faci să vorbești cu ambii deodată? Îi chemi în camera ta. Cele 3 persoane (tu, mama, tata) sunt aceleași, doar că perspectiva este alta. Îi poți vedea simultan.
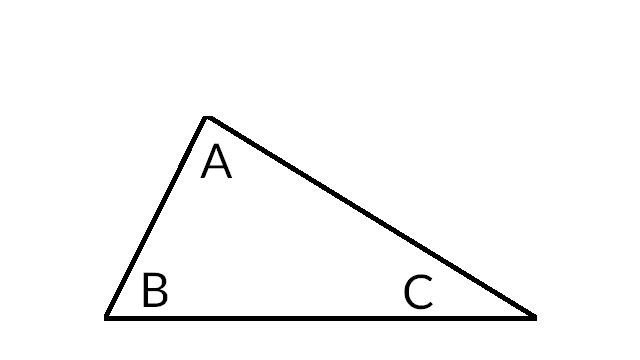
Un exemplu din geometrie – suma unghiurilor unui triunghi. Dacă te uiți la un triunghi, nu-ți dai seama care este suma unghiurilor sale.
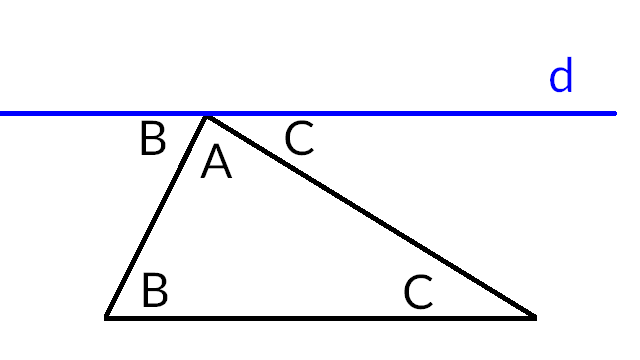
Dar, dacă aliniezi cele 3 unghiuri pe o dreaptă, se vede cu ochiul liber că suma este 180 de grade. Construcția auxiliară este dreapta paralelă la o latură, dusă prin vârful opus acelei laturi.
Distribuția:
A = tu
B = mama ta
C = tatăl tău
dreapta d = camera ta.
Nu orice problemă de geometrie are nevoie de o construcție auxiliară. De multe ori, ce trebuie demonstrat se poate demonstra folosind figura dată.
De unde știi, în general, cum să faci o construcție auxiliară? Nu există o formulă în acest sens. Dar, după ce vezi câteva probleme rezolvate, care folosesc construcții auxiliare, poți încerca acele construcții în problema ta.
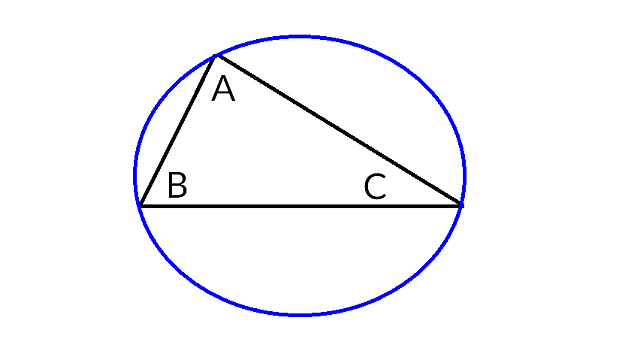
Uneori, aceeași problemă poate fi rezolvată în mai multe moduri, folosind diferite construcții auxiliare în fiecare situație. Adică, poți să-i chemi pe părinți în camera ta, sau puteți discuta toți 3 în sufragerie.
Distribuția:
A = tu
B = mama ta
C = tatăl tău
cercul = sufragerie
(suma unghiurilor = jumătate din suma arcelor care compun un cerc întreg, adică tot 180 de grade).
Dacă vreodată vei găsi o carte în care autorul explică și de ce a făcut acea construcție auxiliară, te rog să-mi spui. Eu n-am reușit să găsesc până acum o astfel de carte. Fără excepție, toate problemele pe care le-am văzut, care folosesc construcții auxiliare au rezolvări de forma : ducem … , după care …. Dar de ce ducem, asta este o taină …